
|
三体問題 天才たちを悩ませた400年の未解決問題 | ||
| 著者 | 浅田 秀樹 | ||
| 出版社 | 講談社 | ||
| サイズ | 新書 |

|
|
| 発売日 | 2021年03月18日頃 | ||
| 価格 | 1,100円(税込) | ||
| ISBN | 9784065228449 | ||
結果として、「三体問題」は厳密な解を与える求積法だけでなく無限級数の形の方法さえも退けてしまったのです。これが、「三体問題は解けない」といわれる所以です。(157ページ)
概要

月は地球の周りを公転しており、その軌道は明らかにはなっているものの、ある時間における正確な位置を計算で求めることができない。これは、月の軌道に地球と太陽の重力が影響しているからである。
月=地球=太陽のように、3つの天体の運動を一般化することを「三体問題」と呼び、天文学・物理学・数学の未解決問題として、数世紀にわたって多くの学者の挑戦をはねのけてきた。20世紀に入り、一般相対性理論が解法をさらに困難にする一方、コンピュータの急速な進化が新たな解法を提供する。
月=地球=太陽のように、3つの天体の運動を一般化することを「三体問題」と呼び、天文学・物理学・数学の未解決問題として、数世紀にわたって多くの学者の挑戦をはねのけてきた。20世紀に入り、一般相対性理論が解法をさらに困難にする一方、コンピュータの急速な進化が新たな解法を提供する。
著者の浅田秀樹さんは、一般相対性理論、重力理論、理論宇宙物理学を専門とする弘前大学大学院の教授だ。
同世代である浅田さんが、あとがきに「筆者が理学部学生だったときに講談社のブルーバックスを楽しく読み漁った人間として、今こうしてその1冊を自分で執筆できることにとても感激しています」(248ページ)と書いた気持ちは、とてもよく理解できる。
同世代である浅田さんが、あとがきに「筆者が理学部学生だったときに講談社のブルーバックスを楽しく読み漁った人間として、今こうしてその1冊を自分で執筆できることにとても感激しています」(248ページ)と書いた気持ちは、とてもよく理解できる。
レビュー

三次方程式の解の公式
第1章・第2章では、解ける方程式と解けない方程式を紹介する。2次方程式の解の公式は、中学の数学で習うのでご存じの通り。4次方程式までは解の公式が存在する。ところが5次以上の方程式には解の公式が存在しない。解の入れ換えの組み合わせの数が大さすぎで、代数的に解くことが不可能になるためだ。

シャルル・エルミート
1858年、数学者のシャルル・エルミート、フランチェスコ・ブリオッシ、レオポルト・クロネッカーが、楕円関数を使った5次方程式の解法を発表した。この方法は「代数的に解くこと」ではない。

ヨハネス・ケプラー
第3章では、ケプラーの法則とニュートンの万有引力の法則を振り返る。ケプラーがティコ・ブラーエの観測記録から発見した法則は、万有引力の法則から導かれる運動方程式によって説明できる。太陽と惑星という「二体問題」の解が、ケプラーの第1法則にある楕円軌道である。
運動方程式は、質量と加速度からなる。質点の位置を微分すると速度になり、速度をさらに微分すると加速度になる。つまり、運動方程式は、物体の位置を表す関数に対する微分方程式となる。
ドイツの数学者カール・フリードリッヒ・ガウスは、観測結果から天体の軌道を求める効果的な軌道計算法を編みだし、1801年に発見され、いったん行方不明になった準惑星ケレスを再発見することに導いた。
運動方程式は、質量と加速度からなる。質点の位置を微分すると速度になり、速度をさらに微分すると加速度になる。つまり、運動方程式は、物体の位置を表す関数に対する微分方程式となる。
ドイツの数学者カール・フリードリッヒ・ガウスは、観測結果から天体の軌道を求める効果的な軌道計算法を編みだし、1801年に発見され、いったん行方不明になった準惑星ケレスを再発見することに導いた。

レオンハルト・オイラー
では、3つの質量が関係する「三体問題」の解法はあるのか――第4章では、前提条件を置く制限三体問題として、レオンハルト・オイラーが「直線解」を発見する。これは、各天体が全体の共通重心のまわりを円運動するものだ。
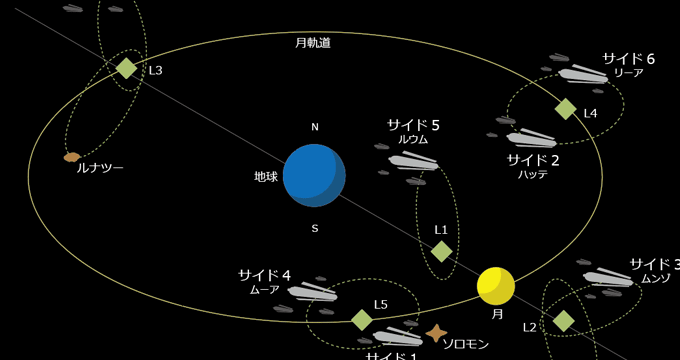
ガンダムのスペースコロニーや小惑星の位置関係
ジョゼフ=ルイ・ラグランジュは、太陽系において直線界が許される場所が複数あることを証明した。アニメ「機動戦士ガンダム」でお馴染みのラグランジュ点である。太陽に比べて非常に軽い惑星と、質量をほぼ無視できる天体(ガンダムでは植民コロニー)の制限三体問題では、ラグランジュポイントの4番目L4と5番目L5が安定する。

アイザック・ニュートン
時代は下り、1906年、太陽と木星に対するラグランジュ点L4とL5に小惑星群「トロヤ群」が発見された。

第5章では、三体問題の一般解を追求する。
ニュートンが発明し、ライピニッツやリーマンによって体系化された積分法は、微分方程式の解を求めることができる。つまり、ニュートンの運動方程式を時間に関して2回積分することができれば、三体問題を解くことができる。これを求積法と呼ぶ。
しかし、三体問題を解くには、17個の互いに独立な「運動の定数」を見つけ出さなければならない。このうち12個はオイラー、ラグランジュ、ヤコビによって発見された。しかし、まだ5個が残っている。
第5章では、三体問題の一般解を追求する。
ニュートンが発明し、ライピニッツやリーマンによって体系化された積分法は、微分方程式の解を求めることができる。つまり、ニュートンの運動方程式を時間に関して2回積分することができれば、三体問題を解くことができる。これを求積法と呼ぶ。
しかし、三体問題を解くには、17個の互いに独立な「運動の定数」を見つけ出さなければならない。このうち12個はオイラー、ラグランジュ、ヤコビによって発見された。しかし、まだ5個が残っている。

アンリ・ポアンカレ
そして1887年、ドイツの天文学者ハインリヒ・ブルンスによって、三体問題に関して互いに独立な「運動の定数」が存在しないことが証明されてしまった。こうして求積法による解法の道は閉ざされた。
さらに1889年、スウェーデン国王兼ノルウェー国王のオスカル2世の60歳の誕生日を祝う懸賞論文として、N体問題を級数展開する課題を提示した。ところが、論文締め切りの直前、フランスの数学者アンリ・ポアンカレは、この課題設定が誤りであることを証明してしまう。
さらに1889年、スウェーデン国王兼ノルウェー国王のオスカル2世の60歳の誕生日を祝う懸賞論文として、N体問題を級数展開する課題を提示した。ところが、論文締め切りの直前、フランスの数学者アンリ・ポアンカレは、この課題設定が誤りであることを証明してしまう。

電子計算機 ENIAC
求積法や級数展開以外の解法はないのか――7章では、20世紀半ばに成長した電子計算機によって、数値演算による三体問題の解法を紹介する。私が電算機の世界に入った時代であり、プログラムで繰り返し計算させることで力任せに微分方程式の数値解が得られるようになった。

8の字解
こうして、3つの天体が十字状の軌道を描くように見える十字解や、8の字ループを描く8の字解が得られる。8の字解はSFのようだが、現実に、銀河あたり1個は存在しているという。

アルベルト・アインシュタイン
第8章では一般相対性理論を取り上げる。
20世紀に入り、天体観測の精度が上がると、水星の近日点が移動していることが明らかになった。この現象はニュートンの運動方程式では説明がつかず、未知の惑星の存在も疑われたが、アインシュタインの一般相対性理論によって決着が付いた。
天体に働く重力は、ニュートンの運動方程式における力ではなく、時間と空間における幾何学(リーマン幾何学)の性質によるものであった。
20世紀に入り、天体観測の精度が上がると、水星の近日点が移動していることが明らかになった。この現象はニュートンの運動方程式では説明がつかず、未知の惑星の存在も疑われたが、アインシュタインの一般相対性理論によって決着が付いた。
天体に働く重力は、ニュートンの運動方程式における力ではなく、時間と空間における幾何学(リーマン幾何学)の性質によるものであった。

空間の歪み
ケプラーの法則やニュートンの運動方程式は近似解であり、より厳密に二体問題を解こうとすると、アインシュタインらによるEIH方程式を解かなければならない。ところが、EIH方程式には、万有引力だけでなく、質量の3次に比例する逆3乗則に従う力もあれば、さらに天体の速度に依存する項まで登場し、厳密に解くことは不可能なものであった。

太陽系
国立天文台が発表している天文暦は、EIH方程式を加味しているとはいえ、あくまで近似的な解となっている。
ここで、小惑星の軌道計算において急に軌道変化する「古在機構」を取り上げているが、『地球は特別な惑星か?』にあるように、太陽系の進化の過程で、木星や土星が太陽に近づいたり遠ざかったりする現象も、EIH方程式によって解き明かされるかもしれない。
近い将来、パソコンを使って太陽系進化の数値計算ができるようになるかもしれない。
ここで、小惑星の軌道計算において急に軌道変化する「古在機構」を取り上げているが、『地球は特別な惑星か?』にあるように、太陽系の進化の過程で、木星や土星が太陽に近づいたり遠ざかったりする現象も、EIH方程式によって解き明かされるかもしれない。
近い将来、パソコンを使って太陽系進化の数値計算ができるようになるかもしれない。
(2021年4月3日 読了)
参考サイト
- 三体問題 天才たちを悩ませた400年の未解決問題:講談社
- アストロメトリ:天文学辞典
- 『地球は特別な惑星か?』:ぱふぅ家のホームページ
- 西暦1619年 - ケプラーの法則:ぱふぅ家のホームページ
- 西暦1666年 - 万有引力の法則:ぱふぅ家のホームページ
- 関数電卓「FX-31」で天体の軌道計算を行う:ぱふぅ家のホームページ
- 西暦1474年 - レギオモンタヌス『天体位置表』:ぱふぅ家のホームページ
- PHPでホロスコープを描く:ぱふぅ家のホームページ
(この項おわり)

